Qu'est-ce que le Business Model Optimizer ?

Encore une expérimentation, qui date d'octobre 2021, et que j'avais trouvée intéressante à l'époque : fournir aux entreprises un outil qui permette de calculer la distance la plus courte vers un objectif de rentabilité. Je n'aurai jamais le temps de développer les mille idées que j'ai toutes les semaines, mais celle-ci en est une que j'ai poussée jusqu'à ce qu'on pourrait appeler un MVP. L'outil est disponible publiquement et gratuitement. Le lien est un peu plus bas. Lisez d'abord pour comprendre comment il s'utilise.

L'idée est de décrire un business model par une bête formule mathématique avec des variables. Dans la formule, chaque variable représente un des paramètres de l'activité d'une entreprise (ou tout autre acteur économique). Par exemple :

• le prix de chaque produit
• le nombre de ventes
• les charges fixes
• les charges variable
• etc...

Votre formule sera en gros un découpage plus fin de :

produits - charge = résultat

Voici un exemple un peu plus complet :

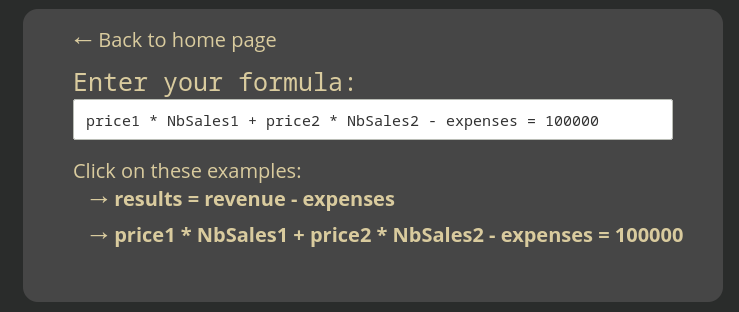
Vous écrivez la formule dans l'outil, en partant de votre situation actuelle. La formule doit donc être à l'équilibre : la valeur de gauche est égale à celle de droite.

L'outil crée alors un champs remplissable pour chacune de ces variables. Vous saisissez les valeurs numériques de ces variables, vos ventes, vos tarifs, vos charges, etc.

Ensuite vous décidez un objectif, typiquement un objectif de résultat.

Pour matérialiser cet objectif, vous changez alors la valeur de la variable résultat directement dans la formule, l'outil recalcule alors toutes les autres variables pour atteindre cet objectif. Vous découvrez donc quel tarif vous devez appliquer, combien de vente vous devez faire, comment modifier vos charges fixes,etc.

Cliquez sur le lien ci-dessous pour essayer :

Business Model Optimizer

Mathématiquement, il s'agit d'un calcul de trajectoire dans un espace de dimension N (N étant le nombre de variables dans votre formule) depuis votre situation actuelle, qui est un point dans cet espace, vers la surface de rentabilité correspondant à votre objectif. La distance est la plus courte mathématiquement.

Dans la vraie vie, la meilleure trajectoire n'est pas forcément la ligne droite, pour des questions de lourdeur ou d'inertie de certaines variables, ou bien pour des questions réglementaires. Vous pouvez donc décrire une trajectoire en plusieurs points selon ce que vous pensez atteignable à court terme. Pour ce faire il suffit de remplacer les variables par des valeurs numériques directement dans la formule et laisser l'outil calculer la nouvelle trajectoire vers le nouveau point d'équilibre que vous avez défini.

Comment ça marche techniquement ?

Le code source est ici : https://github.com/ccomb/bmo

Je vous saoule très brièvement sur la technique. En très bref, il y a un backend en Python, qui utilise une bibliothèque de calcul symbolique (SymPy) et une d'optimisation (scikit-optimize). Le backend stocke les résultats dans une base MongoDB et expose une API grâce à FastAPI. Cette API est interrogée et alimentée via le langage Elm. Toute l'application est une Single Page Application, y compris la landing page, décrite via un fichier texte, analysé par elm-markup, et l'application elle-même est faite via elm-spa et elm-ui pour l'interface.
Ce projet contient donc un certain nombre de choses intéressantes, comme la définition d'un nouveau langage de markup utilisable pour des landing pages, l'utilisation d'une API, celle du calcul symbolique, un calcul d'optimisation dans un espace à N dimensions. Ce n'est pas un projet d'IA, il n'y a pas besoin d'IA pour faire des choses intéressantes. Énormément de problèmes dans les entreprises sont des problèmes d'optimisation.

Pour qui ?

Ce qui est beaucoup moins évident, c'est la question de savoir si ce projet est susceptible d'intéresser quelqu'un en dehors de moi. Si vous pensez que c'est le cas ou si ça vous donne d'autres idées, n'hésitez pas à me contacter pour en discuter, car il y a de nombreuses extensions qu'on peut faire.

Par exemple j'avais commencé à implémenter une notion de « viscosité » de variable pour prendre en compte le fait que des tarifs d'achat ou des charges salariales sont plus difficiles ou plus lentes à modifier que des tarifs de vente ou des charges fixes. J'ai retiré cette fonctionnalité pour garder la solution simple.